判断点 P 是否在三角形 ABC 之内

大家好，我是前端丁修，这篇文章给大家分享一下，如何判断点在三角形内。

为什么这个问题这么重要？

想象一下，你正在开发一个地图应用，用户点击屏幕时，你需要判断点击的位置是否落在某个区域内。这些场景都需要用到点和多边形的位置关系判断，而三角形作为最基本的多边形，是解决这类问题的基础。

几种常用的判断方法

判断点是否在三角形内，常用的有面积法、同向法、重心坐标法、射线法等四种方法。每种方法都有其特点，要根据实际情况选择最合适的方法。

1. 面积法

这个方法特别容易理解，就像小时候玩拼图一样。假设点 P 在三角形 ABC 内部，那么 P 会把三角形分成三个小三角形：PAB、PBC 和 PCA。如果 P 真的在三角形内部，这三个小三角形的面积之和就等于大三角形 ABC 的面积。

面积法

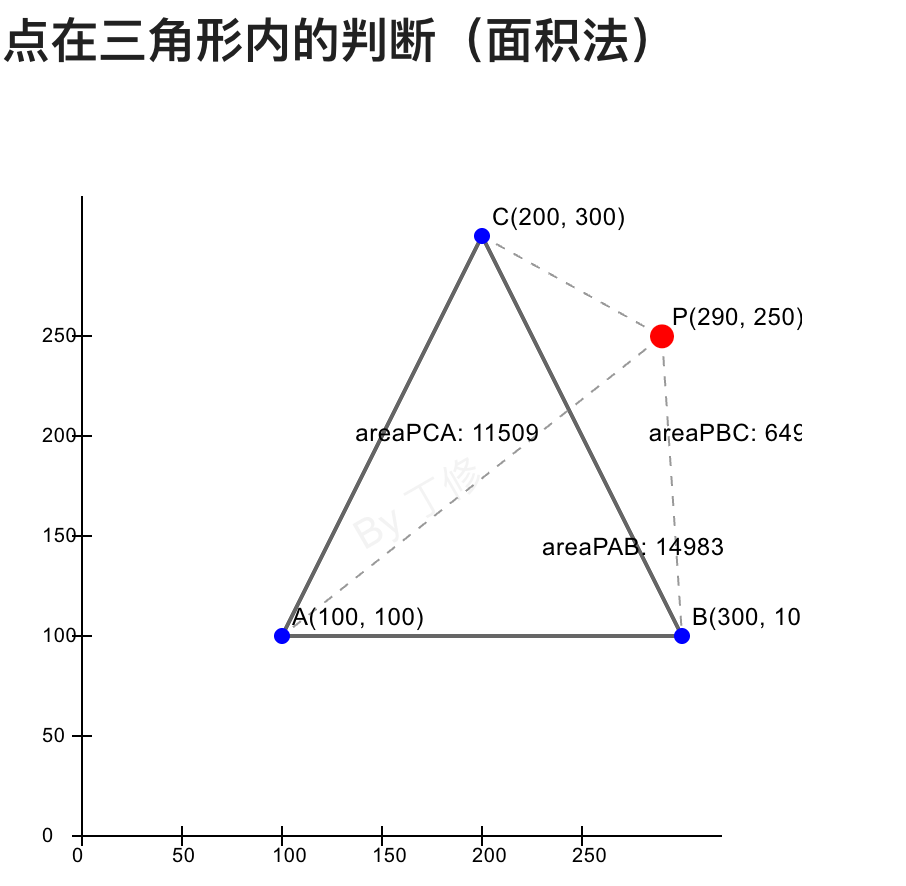
面积法-点在三角形外

来看看具体怎么实现：计算三角形的面积，其实有很多种方法，我们在项目中通常会存储三角形三个点的坐标，所以这里直接根据三角形坐标，使用三角形的面积行列公式计算面积。

typescript
interface Point {
  x: number;
  y: number;
}

// 根据三角形的三个点坐标，计算三角形面积
function calculateTriangleArea(a: Point, b: Point, c: Point): number {
  return Math.abs(
    (a.x * (b.y - c.y) + b.x * (c.y - a.y) + c.x * (a.y - b.y)) / 2
  );
}

typescript
function isPointInTriangleByArea(
  p: Point,
  a: Point,
  b: Point,
  c: Point
): boolean {
  const areaABC = calculateTriangleArea(a, b, c);
  const areaPAB = calculateTriangleArea(p, a, b);
  const areaPBC = calculateTriangleArea(p, b, c);
  const areaPCA = calculateTriangleArea(p, c, a);

  return Math.abs(areaABC - (areaPAB + areaPBC + areaPCA)) < 0.001;
}

这个方法的优点是特别直观，代码也容易理解。不过计算量相对大一些，因为要计算四个三角形的面积。

2. 同向法

我们用向量叉积来判断方向，向量叉积（Cross Product）是向量运算中的一种，用于判断两个向量的相对方向。

这个方法的思路是通过向量叉积来判断点 P 相对于三角形三条边的位置。如果点 P 相对于每条边的叉积符号相同（都为正或都为负），则点 P 在三角形内部；否则，点 P 在三角形外部。

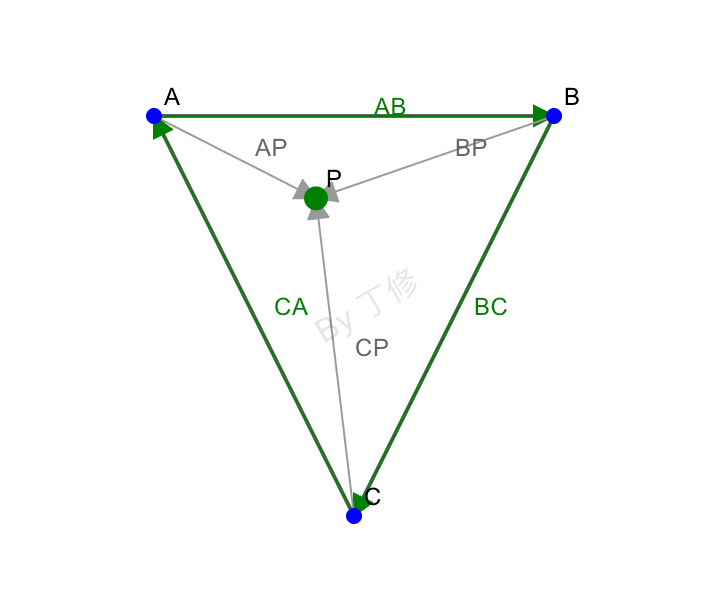
同向法点在三角形内

同向法点在三角形外

具体来说：

如果点 P 在边 AB 的左侧，则向量叉积 calcCrossProduct(a, b, p) 为正值。如果点 P 在边 AB 的右侧，则向量叉积 calcCrossProduct(a, b, p) 为负值。如果点 P 在边 AB 上，则向量叉积 calcCrossProduct(a, b, p) 为零。同理，我们可以计算点 P 相对于边 BC 和边 CA 的叉积。如果点 P 相对于三条边的叉积符号相同（都为正或都为负），则点 P 在三角形内部；否则，点 P 在三角形外部。

typescript
// 计算向量的叉积
function calcCrossProduct(a: Point, b: Point, p: Point): number {
  // |  (b.x - a.x)  (p.x - a.x) |  | ABx  APx |
  // |  (b.y - a.y)  (p.y - a.y) |  | ABy  APy |
  return (b.x - a.x) * (p.y - a.y) - (b.y - a.y) * (p.x - a.x);
}

function isPointInTriangleByCrossProduct(
  p: Point,
  a: Point,
  b: Point,
  c: Point
): boolean {
  const ab = calcCrossProduct(a, b, p); // AB AP
  const bc = calcCrossProduct(b, c, p); // BC BP
  const ca = calcCrossProduct(c, a, p); // CA CP

  return (ab >= 0 && bc >= 0 && ca >= 0) || (ab <= 0 && bc <= 0 && ca <= 0);
}

这个方法的计算效率比面积法高，而且实现起来也不复杂。

3. 重心坐标法

重心坐标法是一种判断点是否在三角形内部的有效方法。它基于将点表示为三角形顶点的线性组合。通过计算点在三角形顶点的权重，我们可以确定点是否在三角形内部。具体步骤如下：

重心坐标的定义

重心坐标（Barycentric Coordinates）是一种在三角形内部表示点位置的坐标系统。对于任意一个三角形 ABC 和其中的一个点 P，重心坐标使用三个权重(λ1, λ2, λ3)来表示，这三个权重就是重心坐标。公式为：

$P = \lambda_1 \cdot A + \lambda_2 \cdot B + \lambda_3 \cdot C$

重心坐标的推导

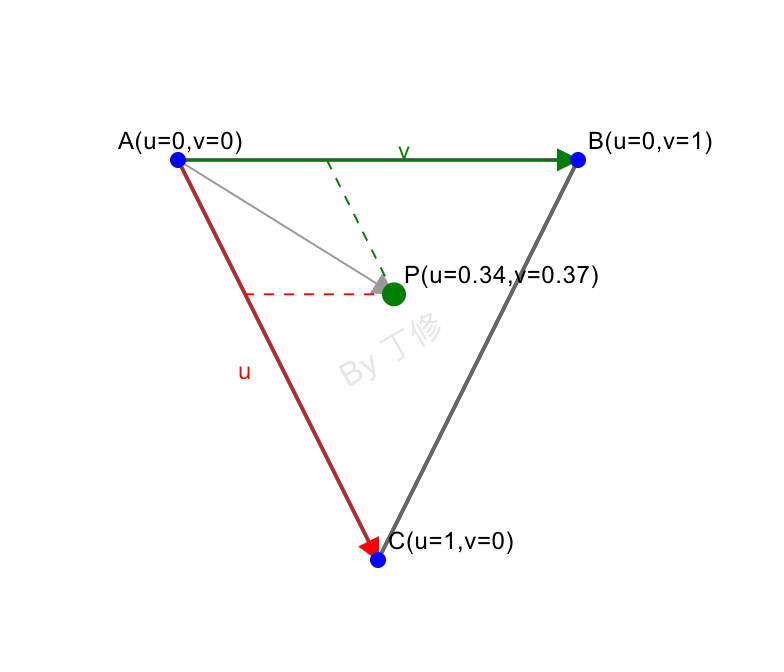
重心坐标法
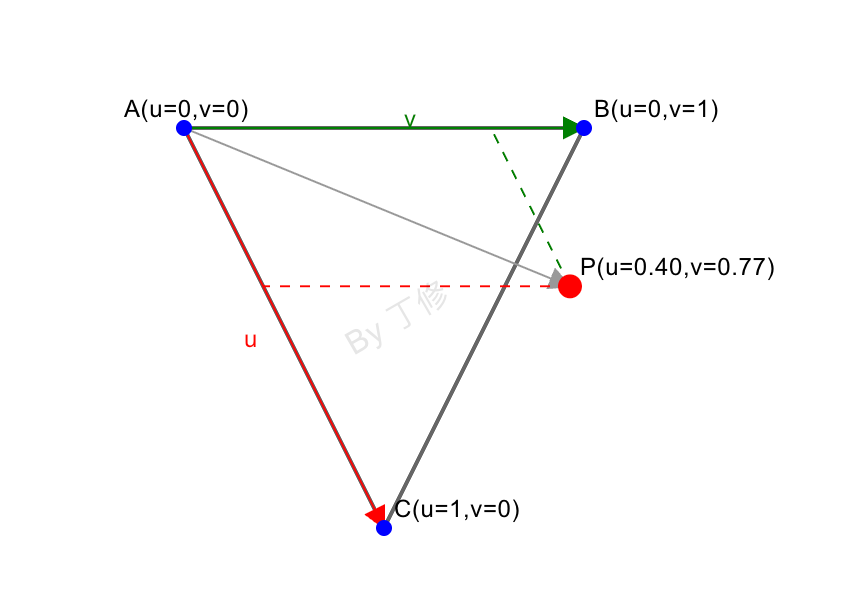
重心坐标法，点在三角形外

在同一平面内，三角形的三个顶点 ABC 中若选定一点 A 作为基点，则 B 与 C 可视为相对 A 的位移。对于该平面上任意一点 P，都可通过下式表示：

P = A + u(C – A) + v(B – A)

若将系数 u、v 取负数，即表示沿相反方向移动；若要使 P 位于三角形内部，则需满足：

u ≥ 0
v ≥ 0
u + v ≤ 1

当 u=0 且 v=0 时，P 落在点 A；当 u=0, v=1 时，P 在点 B；当 u=1, v=0 时，P 在点 C。

令 v0 = C – A（表示从点 A 到点 C 的向量）、v1 = B – A（表示从点 A 到点 B 的向量）、v2 = P – A（表示从点 A 到点 P 的向量），则有 v2 = u·v0 + v·v1。将等式两边分别与 v0、v1 做点乘，便得到：

v2 • v0 = u(v0 • v0) + v(v1 • v0)
v2 • v1 = u(v0 • v1) + v(v1 • v1)

可将这组方程视作线性方程组并使用行列式求解。
令 a = (v0•v0), b = (v1•v0), c = (v0•v1), d = (v1•v1)，p = (v2•v0), q = (v2•v1)。

两式写成矩阵乘法形式：
[ a b ] [ u ] = [ p ]
[ c d ] [ v ] = [ q ]

行列式 det = ad - bc。矩阵逆为 (1/det)·[ d -b; -c a ]，因此有：
u = (1/det) · ( d·p - b·q )
v = (1/det) · ( -c·p + a·q )

将 a、b、c、d、p、q 换回原始点积，即得：
u = [(v1•v1)(v2•v0) - (v1•v0)(v2•v1)] / [(v0•v0)(v1•v1) - (v0•v1)(v1•v0)]
v = [(v0•v0)(v2•v1) - (v0•v1)(v2•v0)] / [(v0•v0)(v1•v1) - (v0•v1)(v1•v0)]

代码如下

typescript
// 函数接收四个参数，分别是点 p 和三角形的三个顶点 a、b、c，
function isPointInTriangle(p: Point, a: Point, b: Point, c: Point): boolean {
  // 向量 AC
  const v0 = { x: c.x - a.x, y: c.y - a.y };
  // 向量 AB
  const v1 = { x: b.x - a.x, y: b.y - a.y };
  // 向量 AP
  const v2 = { x: p.x - a.x, y: p.y - a.y };
  // 这些点积用于计算重心坐标（barycentric coordinates），以确定点 P 是否在三角形内。
  // 计算五个点积：dot00、dot01、dot02、dot11 和 dot12。
  // dot00 是向量 v0 与自身的点积，表示 v0 的长度平方。
  const dot00 = v0.x * v0.x + v0.y * v0.y;
  // dot11 是向量 v1 与自身的点积，表示 v1 的长度平方。
  const dot11 = v1.x * v1.x + v1.y * v1.y;

  // dot01 是向量 v0 与 v1 的点积，表示 v0 和 v1 之间的夹角关系。
  const dot01 = v0.x * v1.x + v0.y * v1.y;
  // dot02 是向量 v0 与 v2 的点积，表示 v0 和 v2 之间的夹角关系。
  const dot02 = v0.x * v2.x + v0.y * v2.y;
  // dot12 是向量 v1 与 v2 的点积，表示 v1 和 v2 之间的夹角关系。
  const dot12 = v1.x * v2.x + v1.y * v2.y;

  const invDenom = 1 / (dot00 * dot11 - dot01 * dot01);
  const u = (dot11 * dot02 - dot01 * dot12) * invDenom;
  const v = (dot00 * dot12 - dot01 * dot02) * invDenom;

  return u >= 0 && v >= 0 && u + v < 1;
}

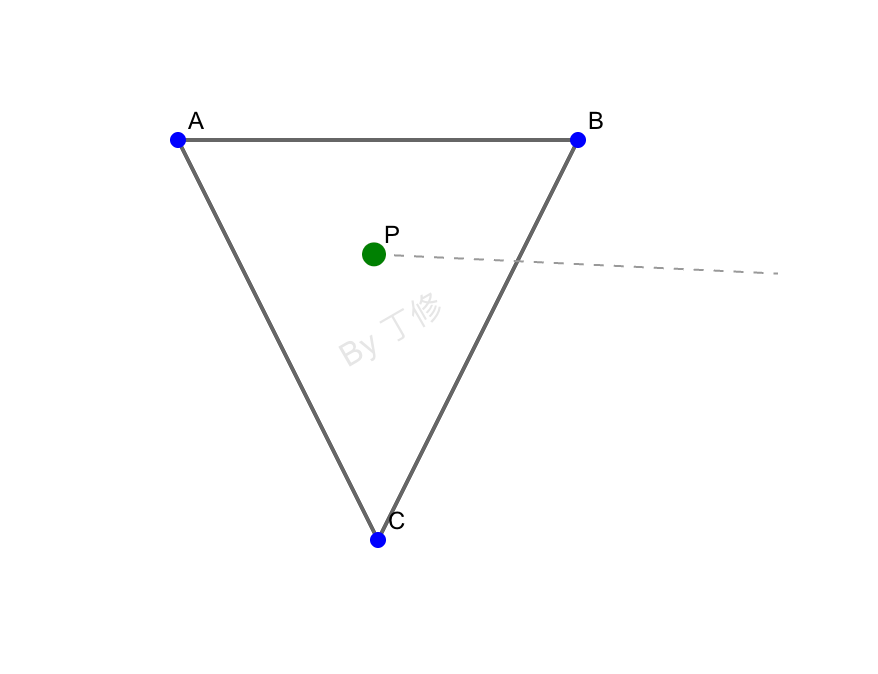
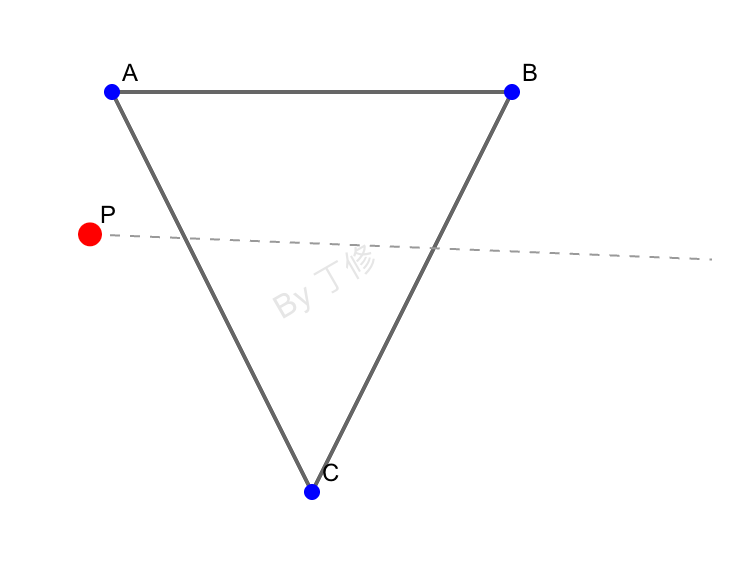
4. 射线法

从点 P 向任意方向发射一条射线，统计它和三角形边的交点个数。如果交点个数是奇数，说明点在三角形内部；如果是偶数，说明在外部。

射线法

射线法点在三角形外

typescript
 

// 判断点是否在三角形内的射线法实现
 // 计算叉积
export function crossProduct(a: Point, b: Point, c: Point): number {
  return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
}

// 判断线段是否相交
function isIntersect(
  p1: Point, p2: Point,  // 第一条线段的端点
  p3: Point, p4: Point   // 第二条线段的端点
): boolean {
  // 完全不相交
  if (Math.max(p1.x, p2.x) < Math.min(p3.x, p4.x) ||
      Math.max(p3.x, p4.x) < Math.min(p1.x, p2.x) ||
      Math.max(p1.y, p2.y) < Math.min(p3.y, p4.y) ||
      Math.max(p3.y, p4.y) < Math.min(p1.y, p2.y)) {
    return false;
  }

  // 跨立实验
  const cross1 = crossProduct(p1, p2, p3) * crossProduct(p1, p2, p4);
  const cross2 = crossProduct(p3, p4, p1) * crossProduct(p3, p4, p2);
  return cross1 <= 0 && cross2 <= 0;
}

// 使用射线法判断点是否在三角形内
export function isPointInTriangleByRay(
  p: Point,
  triangle: Triangle
): {
  isInside: boolean;
  intersections: {
    ab: boolean;
    bc: boolean;
    ca: boolean;
  };
} {
  const { a, b, c } = triangle;
  
  // 创建一条向右的射线
  const ray = {
    x: p.x + 1000, // 足够长的射线
    y: p.y
  };

  // 检查与三条边的相交情况
  const intersectAB = isIntersect(p, ray, a, b);
  const intersectBC = isIntersect(p, ray, b, c);
  const intersectCA = isIntersect(p, ray, c, a);

  // 统计交点个数
  const intersectCount = (intersectAB ? 1 : 0) + 
                        (intersectBC ? 1 : 0) + 
                        (intersectCA ? 1 : 0);

  return {
    isInside: intersectCount % 2 === 1,
    intersections: {
      ab: intersectAB,
      bc: intersectBC,
      ca: intersectCA
    }
  };
}

实际应用中的注意事项

在实际使用这些方法时，有几点需要特别注意：

浮点数精度问题：由于计算机浮点数的精度限制，判断相等时要留有一定的误差范围。
边界情况：点在三角形边上或顶点上时的处理要特别小心。
性能考虑：在需要大量计算的场景下，建议使用同向法或重心坐标法。

希望这篇文章对大家有帮助！

目录