如何判断一个点是否在一个凸多边形内

大家好，我是前端丁修，今天我们来学习如何判断一个点是否在凸多边形内。这是图形处理中经常遇到的问题，也是面试中的常见问题。

首先，我们讨论的是凸多边形。什么是凸多边形呢？简单来说，就是所有内角都小于 180 度的多边形，看起来没有"凹进去"的部分。虽然本文标题是关于凸多边形的判断，但其中的引射线法实际上对任意多边形（包括凹多边形）都适用。面积法和夹角法则主要适用于凸多边形。

接下来，我会介绍几种常用的方法，包括面积和判别法、夹角和判别法以及引射线法。

面积和判别法

基本原理

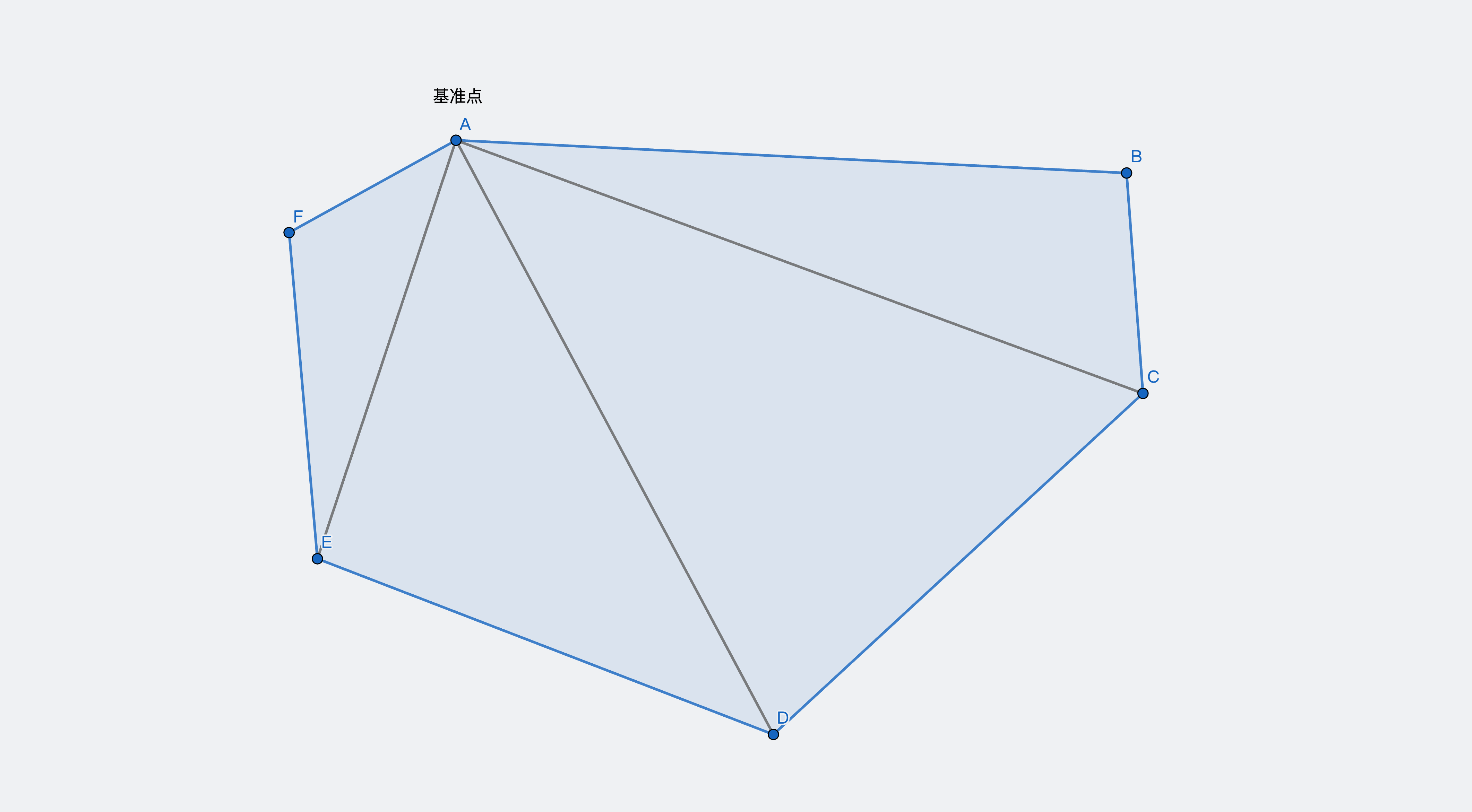
第一种方法是用面积来判断：如果点在多边形内部，那么这个点和多边形的每条边组成的小三角形的面积之和，应该等于整个多边形的面积。

三角形面积可以通过向量叉积计算：

详细步骤

1. 计算多边形的总面积。可以通过以下方式计算:

   • 选择多边形的一个顶点作为基准点
   • 将多边形分割成多个三角形
   • 对每个三角形使用向量叉积计算其有向面积
   • 将所有三角形的面积相加得到多边形总面积 注意：向量叉积得到的是有向面积，需要取绝对值才是真实面积

2. 计算点与多边形各顶点形成的三角形面积之和。

3. 比较总面积与三角形面积之和，如果相等，则点在多边形内，这里要考虑容差。

示例代码

typescript
// 计算三角形面积的函数
function triangleArea(p1: [number, number], p2: [number, number], p3: [number, number]): number {
  const [x1, y1] = p1;
  const [x2, y2] = p2;
  const [x3, y3] = p3;
  return Math.abs((x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1)) / 2;
}

function isPointInsidePolygonArea(polygon: [number, number][], point: [number, number]): boolean {
  let totalArea = 0;
  let sumAreas = 0;
  const n = polygon.length;

  // 计算多边形总面积
  for (let i = 0; i < n; i++) {
    const j = (i + 1) % n;
    totalArea += triangleArea(polygon[0], polygon[i], polygon[j]);
  }

  // 计算点与各边构成的三角形面积和
  for (let i = 0; i < n; i++) {
    const j = (i + 1) % n;
    sumAreas += triangleArea(point, polygon[i], polygon[j]);
  }

  // 考虑JS浮点数精度问题
  return Math.abs(totalArea - sumAreas) < 1e-10;
}

夹角和判别法

基本原理

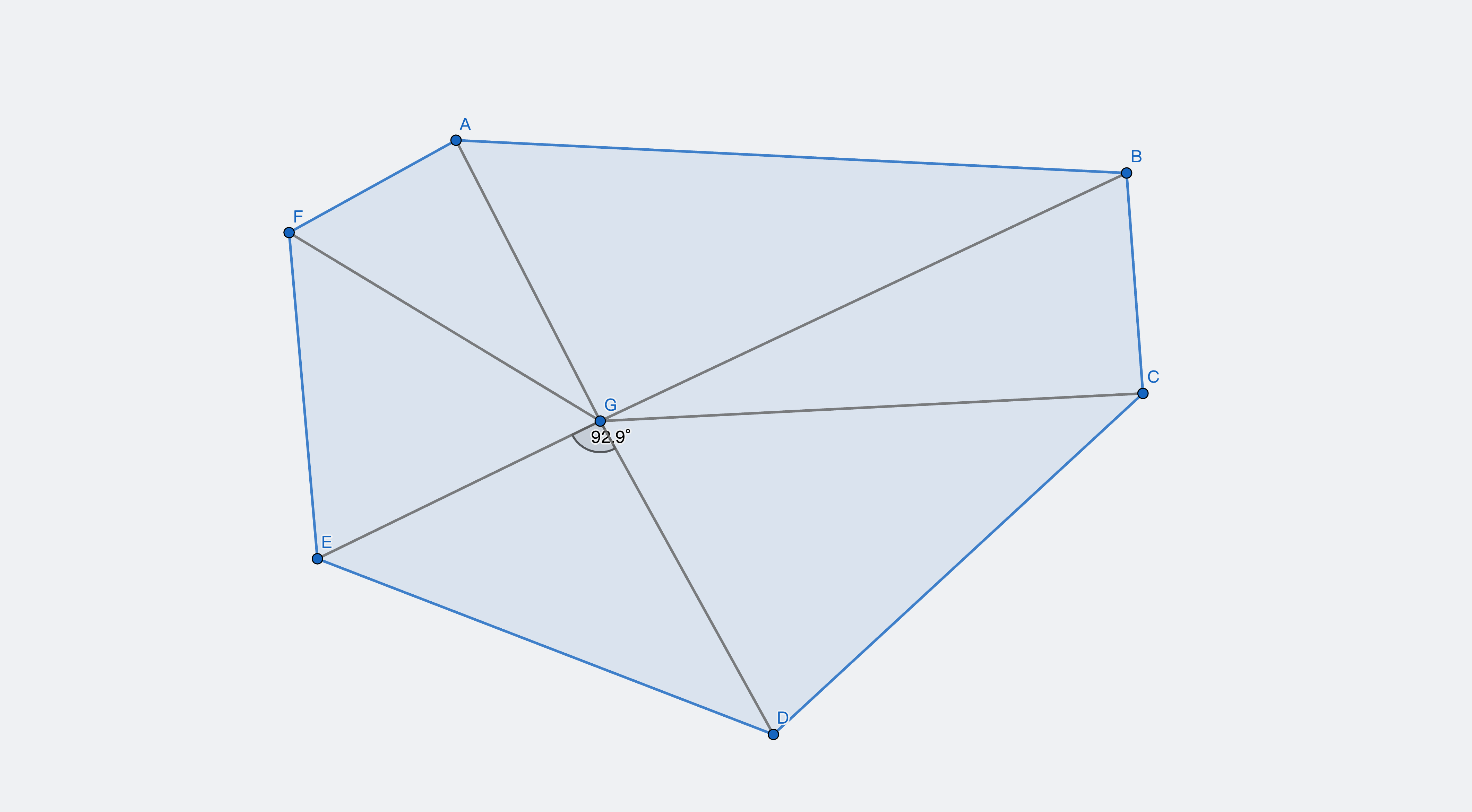
第二种方法是看夹角。如果一个点在多边形内部，那么这个点与多边形各顶点的向量之间的夹角之和应该等于 360 度。这就是夹角和判别法的核心思想。

详细步骤

1. 计算点与多边形各顶点的向量。
2. 计算相邻向量之间的夹角。
3. 判断夹角之和是否为 360 度。

示例代码

typescript
// 计算两个向量之间的夹角
// v1, v2: 两个二维向量
// 返回值: 两个向量的夹角(弧度)
function vectorAngle(v1: [number, number], v2: [number, number]): number {
  // 计算点积
  const dotProduct = v1[0] * v2[0] + v1[1] * v2[1];
  // 计算叉积
  const crossProduct = v1[0] * v2[1] - v1[1] * v2[0];
  // 使用atan2计算夹角,范围为[-π,π]
  return Math.atan2(crossProduct, dotProduct);
}

// 使用夹角和判别法判断点是否在多边形内
// polygon: 多边形顶点数组
// point: 待判断的点
// 返回值: 点是否在多边形内
function isPointInsidePolygonAngle(polygon: [number, number][], point: [number, number]): boolean {
  let angleSum = 0; // 夹角和
  const n = polygon.length; // 多边形顶点数

  // 遍历多边形的每条边
  for (let i = 0; i < n; i++) {
    // 计算point到当前顶点的向量
    const v1: [number, number] = [polygon[i][0] - point[0], polygon[i][1] - point[1]];
    // 计算point到下一个顶点的向量
    const v2: [number, number] = [
      polygon[(i + 1) % n][0] - point[0],
      polygon[(i + 1) % n][1] - point[1],
    ];
    // 累加两个向量的夹角
    angleSum += vectorAngle(v1, v2);
  }

  // 判断夹角和是否接近2π(考虑浮点数误差)
  return Math.abs(Math.abs(angleSum) - 2 * Math.PI) < 1e-10;
}

引射线法

基本原理

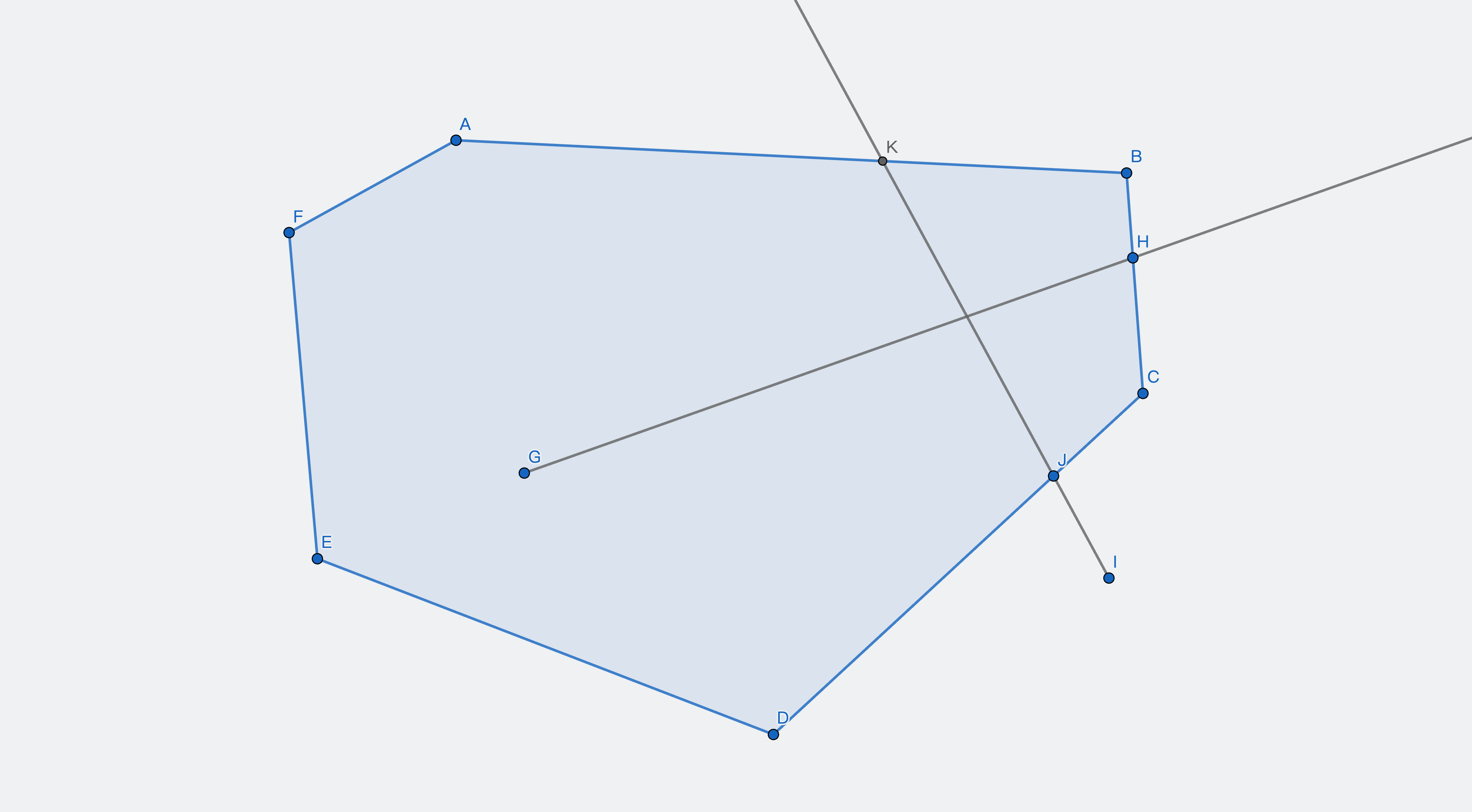
最后一种方法原理是这样的：从点画一条射线线，看这条线和多边形边界相交多少次。如果是奇数次，说明点在内部；偶数次说明在外部。

详细步骤

• 从点向任意方向引射线。
• 计算射线与多边形边的交点数。
• 判断交��数是否为奇数。

示例代码

typescript
// 使用射线法判断点是否在多边形内
// polygon: 多边形顶点数组
// point: 待判断的点[x,y]
// 返回值: 点是否在多边形内
function isPointInsidePolygonRay(polygon: [number, number][], point: [number, number]): boolean {
  // 获取待判断点的坐标
  const [x, y] = point;
  // inside表示点是否在多边形内
  let inside = false;

  // 遍历多边形的每条边
  // j表示当前边的起点索引,i表示终点索引
  for (let i = 0, j = polygon.length - 1; i < polygon.length; j = i++) {
    // 获取边的两个端点坐标
    const [xi, yi] = polygon[i];
    const [xj, yj] = polygon[j];

    // 判断射线是否与当前边相交
    // 条件1:点的y坐标在边的两个端点y坐标之间
    // 条件2:点的x坐标小于射线与边的交点的x坐标
    if (yi > y !== yj > y && x < ((xj - xi) * (y - yi)) / (yj - yi) + xi) {
      // 如果相交则改变inside的值
      inside = !inside;
    }
  }

  return inside;
}

5. 实际应用建议

这三种方法各有优缺点：

• 面积法：好理解，好实现，但有浮点数误差，适用于需要快速判断且对精度要求不是特别高的场景
• 夹角法：精确度高，但计算量大，涉及三角函数，适用于需要同时计算其他几何特征的场景
• 引射线法：通用性强，精度较好，实现相对复杂，适用于要求高精度的场景，特别是处理边界情况时

在实际开发中，要注意这些坑：

• JS 的浮点数精度问题，所以判断相等时要用一个很小的误差值
• 点正好在多边形边上的情况要特别处理
• 多边形顶点的顺序最好是顺时针或逆时针，不要乱序

以上介绍了三种判断点是否在凸多边形内的方法：面积和判别法、夹角和判别法以及引射线法。每种方法都有其优缺点，大家可以根据实际需求选择合适的方法。希望这篇文章对你有所帮助！